
Donna Bergmark
Cornell Theory Center
(presented at Super '96 in Ames, Iowa)
HPF Languge processors are listed here pretty much in order of market introduction. It is probably not a complete list. The primary research compilers are, of course, Fortran D at Rice, Vienna Fortran, and the one at Syracuse. Adaptor is in the public domain, and has a reasonable reputation.
You do not have to code in Fortran 90 (and I will soon show you an example that is tough on ``real'' HPF compilers). But if you do use the data parallel constructs in F90 and the new FORALL construct in F95, you will help the compiler optimize your code.
What about calling MPI from HPF/F90? You can do this as long as you don't try to pass fancy array sections across the calling boundary. Most stuff works fine. ECMWF codes call MPI from F90 with no problems (but they stay within certain language constructs). Of course, you will want to put the MPI calls inside EXTRINSIC subroutines.
Can you use C, C++? Yes, in EXTRINSIC subroutines. The IBM documentation has examples of this.
What if you don't have an F90 compiler? (SP2 users are so lucky, because xlf supports both). Could use one of the preprocessors and keep the F77 code that comes out.
t1=mclock() ! CPU time in .01 secs
do i = 1,1000 ! timing loop
itc = 0
!!HPF$ INDEPENDENT
do j = 1, ndemm
do 250 k = 1, nsupm
if (apatho(k, j) .gt. 0.) itc = itc + 1
250 continue
enddo
end do
t2 = mclock()
This is the original version of a loop contained in a Fortran 77 program. It is a reduction loop that can be run in parallel; and in fact the FORGE toolset inserted an INDEPENDENT directive in front of the loop to say that; we have commented it out for correctness (you cannot assign to the same object in different iterations of the loop and still call it INDEPENDENT).
We have used mclock() to get CPU time for the loop, and there is a timing loop (DO i = 1,1000) just to measure the times.
The main part of the loop is the "do j-do k" part. APATHO is a partitioned array (on the j index) and we want "do j" to be run in parallel. The loop counts up the number of positive elements of APATHO. Timing results showed no speedup as we added processors.
...So, we replaced the IF with an intrinsic ...
t1=mclock()
do i = 1,1000
itc = count (apatho(:nsupm, :ndemm) .gt. 0.)
end do
t2 = mclock()
Here, we have replaced the reduction loop with a call to the F90 intrinsic, COUNT, which returns the number of .TRUE values in a logical array. The logical array in question is the temporary,
apatho(:nsupm, "ndemm) .gt. 0

To the programmer, both versions are semantically equivalent, but not to the compiler. Look at the timing results to see what this small recoding does.
(By the way, we observed the same effect with several HPF compilers.)
And for replicated loops (e.g. counting up elements from non-partitioned arrays) it is not unusual for the intrinsic to run 2X faster than the DO loop with an IF in it. No speedup, of course.
for all years do +---+---+------+---+ | | | ... | | +---+---+ +---+ "compute air, earth, : : : : : water, temp, etc." +---+---+ ... +---+ | | | | | +---+---+------+---+ global update of the forest end do
Here is the pseudo-code for a forest simulation model which is inherently data parallel but expressed in Fortran 77 syntax.
In fortran 77 syntax, the square is represented by a double loop nest that iterates over each row within each column calling routine AIR(i,j), WATER(i,j) etc. to update that plot. Thus the loop body is 6 subroutine calls. Information computed by AIR for plot (i,j) is passed on to the WATER for plot (i,j) routine via COMMON.
The objective is to convince HPF that the iterations are independent.
So, what do we do? Ideally, we would declare the loopnest to be INDEPENDENT and the called subroutines PURE (i.e. no side-effects) and the compiler would parallelize the nest.
But if all else fails ...
So, how would we convert that Forest problem? Here's one way:
for all years do
call hpf_local with my share of the plots
globally update the forest (in replication)
end
Each node runs original F77 loop nest on the data it is given,
which is essentially a sub-division of the forest. No changes
within the program. But you have a REALLY LONG argument list.

This illustrates what happens when you pass an HPF array to an EXTRINSIC procedure. Here, Y is a very large array distributed over the memory of six processors. One instance of the Extrinsic routine gets its piece of the array.
What should the compiler do for you? Collect together the bits of the array (e.g. cyclic distribution is sequential memory by time you get to the routine); likewise upon exit it should redistribute; and smart compilers will obey the INTENT(IN) and INTENT(OUT) descriptions in the F90 interface block for the Extrinsic procedure.
You now begin to have an idea of the things a compiler can do for you. HPF directives are hints to the compiler to guide its work. For example, how to co-locate the data.
I've not yet seen a compiler ignore a DISTRIBUTE directive. But I have seen plenty who ignore INDEPENDENT directive on a DO loop. Mainly, the compiler adds distributions.
How do compiler implementations vary from each other? (Next Slide).
One question that might come up under the heading of ``What to expect from an HPF compiler'' is how do HPF compilers vary in those not inconsequential number of areas where things are left to the implementation? In fact, there are surprisingly few variations. (Maybe because of the ``advice to implementors'' scattered throughout the language specification.)
EXTRINSIC kind keywords vary the most - HPF_LOCAL and HPF_SERIAL are defined in the standard. Beyond that you get F77_LOCAL, CRAFT_LOCAL, ...
APR's processor is quite distrinctive (idiosyncratic, some would say) in many respects: data layout, additional directives of their own and a special EXTRINSIC called SAFE EXTRINSIC.
Non-distributed data (also called ``implicitly mapped'' by the word-loving HPFF) is handled in different ways because HPF 1.1 is fairly mute on the subject. Mostly you can expect scalars and arrays that are never mentioned in any HPF directive to be treated as private. Or at least node-local. The compiler could choose to map these variables in a way it sees fit, but I have not seen it.
You can always expect node 0 to do the input and output (as opposed to some other node number).
How the computation is distributed can be a big difference. The standard says that ``In all cases, users should expect the compiler to arrange the computation to minimize communication while retaining parallelism.'' In my experience, the ``owner computes'' rule has been used exclusively, regardless of how many off-node elements you are using. Also in my experience, this works out perfectly well.
The last phrase is because single node execution is what minimizes communication ... along with parallelism.
HPF compilers spend much more of their optimizing dollars on how to minimize communication, though this might be different for shared memory HPF compilers.
Minimizing communications is, in fact, the hallmark of a GREAT HPF compiler.
HPF 1.1: ``Vendors are allowed to implement any I/O extensions to the language they may wish.''
Have I seen any Parallel I/O? Nope.
But EXTRINSIC works fine.
Here is how we have dealt with the problems of I/O bottleneck and with memory space restrictions.
! read in tariff data
do 78 i = 1, nsupm
do 88 j = 1, ndemm
read (TARUNIT, 98) tar(i, j)
98 format (f10.3)
88 continue
78 continue
Problem: There were 8 MB of data in all!
Solution: EXTRINSIC data input routine into
SEQUENCE variables.
One element of up to 8 MBytes of data is read at a time, on node 0. Because of sequential semantics, these cannot be vectored up. So a value is read, and then sent out to whatever node ``owns'' it. At 2 million numbers, this gets to be slow, especially with replicated data, as the number of processors increases.
Solution: have all nodes read in the data, in parallel, from shared file space or from temp, by turning all the input statements into an EXTRINSIC procedure.
Data is passed back to the HPF caller either by arguments or by SEQUENCE variables in COMMON.
The node can use inquiry routines (such as my_processor()) to find out who it is and read in only the part of the global array that is resident on this node.
For example ... see next slide.
write(u) AA is an array, 750 Mbytes in size. (Whoops!)
Solutions:
Here is a memory bottleneck due to I/O.
The first thing that happens as that not all 750 MBytes will fit on node 0. The second thing that happened is that not more than 256 MBytes could be in a single binary write.
The compiler cannot protect you here, again because of sequential semantics. But it is easy to get around: The first solution writes to a bunch of little files. If you don't like that, then use the second solution - write out A(i) for i = 1, number_of_processors(). Single communication to get a block of data to node 0; minimum number of writes.
do j = 1, ndemm
demp(j) = dhxlin(j)
do 1187 k = 1, ncr
demp(j) = demp(j) + dslope(j, k) * demand(ind2(j, k))
end do
end do
This is the first remark anybody ever makes about HPF, especially if they don't want to use HPF. But here is an example of a loop which is perfectly well handled by most HPF compilers, even though it uses indirect addressing.
The first thing that people say they mean by ``irregular" is indirect addressing. But in this example, assuming demp, dslope, demand, and ind2 are all partitioned arrays, the loop can be run in parallel, on j.
Some compilers will bring all of demand on-node before the loop starts and index in parallel; others will fetch one element at a time inside the k loop, in which case your performance tuning tweak is to make a replicated array called ``temp" and assign temp := demand before entering the loop, and then using temp.
Either way it may be irregular, but it is not unmanageable.
gdiff = 0
:
if (diff > gdiff) gdiff = diff
BUT:
giff = maxval (OLD - NEW) ! array operation
What kind of optimizations can you expect from an HPF compiler?
They should be able to optimize communications. e.g.IBM's compiler and APR's preprocessors can vectorize communications - bring them outside a loop. Tracing tools tell you when communication is happening within the loop.
Avoid artificial sequential dependences. A really good compiler would be able to figure out the following, but for now you often have to do the array expansion yourself.
One consequence of compiler optimization is that small changes in the source can produce large changes in performance (CYCLIC vs. BLOCK; rows vs. columns; loop inhibitors)
You should expect compilers to generate reports or intermediate code, which you can read to see exactly what compiler did or did not do for you. Either ``real'' or pseudo Fortran.
To continue, certainly if you are using HPF mainly to partition your data and keep track of what's on what processor, we hope your data is stored in arrays.
Dynamic load balancing, often used as an excuse not to use HPF, need not be a problem. For example, the prefix scan algorithms developed for the Thinking Machines can be very useful.
Data locality is the problem: if you cannot replicate the problem data (because of insufficient memory), then you cannot shift the work around without shifting the data as well.
If you know your algorithm well, you can have HPF call MPI routines. You can escape HPF semantics when the need arises. Upon return to HPF, the contents of the local portion of the array may have changed (via an MPI scatter-gather, e.g.).

As the previous slide showed, it is quite possible for HPF performance to approach that of hand-coded MPI. It usually is not as bad as the 2X ratio that Ken Kennedy often hoped for.
That being said, it is true that you will probably need to alter your code in order to achieve performance with ``real'' HPF compilers. (An exception is the APR compiler with its IGNORE DEPENDENCES directive.)
Variance in performance can bo do to:
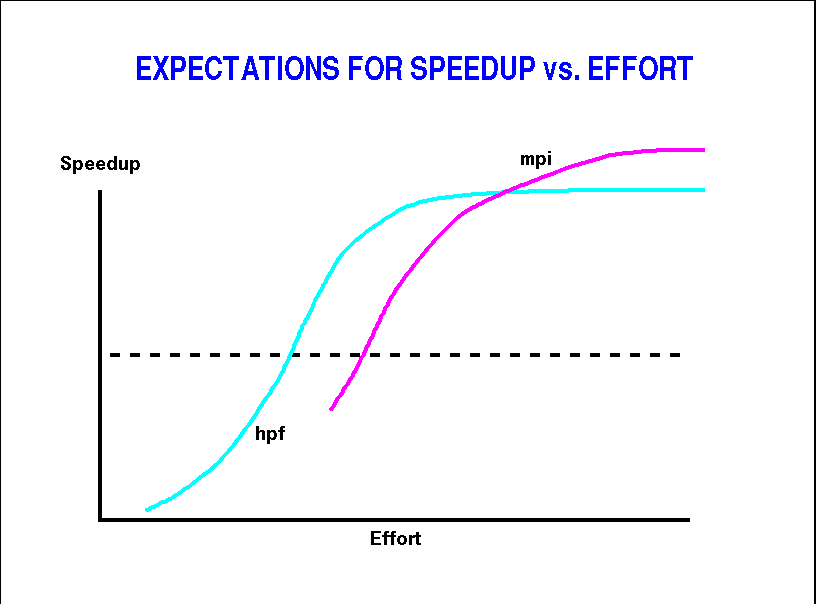
As with all parallel codes, your first attempt is almost certain to get slowdown. And there comes a point beyond which it doesn't pay to optimize more. That is shown in the two curves here.
Unlike MPI, where your effort will be to getting the right answer, (or even to get it running), with HPF your effort will be to get acceptable performance.
The initial speedup will probably be awful. It is pretty hard to convince some HPF compilers to parallelize loops. The ultimate performance is a little lower, the knee a little closer, but you get there with the same effort (or less) than with MPI, depending on the degree to which your program is data parallel.
HPF is certainly mor concise (the number of directives added to tariff is on the order of 10, including an interface block; for the MPI code, it can be pages. And if you are using a source-to- source translator, 2 pages of HPF can become 30 pages of message-passing with calls to vendor code.
I'd like to say that HPF is the closest thing to automatic parallelism but it is not. You will spend as much time designing a well-performing HPF code as you will an MPI code.
If you have regular arrays, HPF will do all the housekeeping for you: which iterations to run on this processor, alignment of data, when to communicate, how to calculate addresses and the like.
This is a good research project - I do not really know how well XL HPF will scale, as we have AIX 4.1 only on 12 nodes. In theory, this slide relates to the scaling characteristics of HPF.
One topic that comes under the rubric of performance is ``scalability'' of the compiled code. With the exception of node 0 I/O and of HPF_SERIAL routines, HPF-generated code is scalable.
Because it is single-threaded, one can imagine that group communications and log n global reductions are the norm.
HPF runs on as few processors as 1 and as many processors as the application warrants. Distributed arrays (in my experience) are stored in what APR calls ``shrunk'' form, so memory costs scale with the size of the job. The number of processors is defined at run time (number_of_processors()) and F90 supports dynamic memory allocation.
The main ``hit'' you will see on scalability is that due to the extra parallel overhead you get in an HPF-compiled code (memory copies, temporary allocation and deallocation) the ultimate speedup will be less than hand-coded MPI, and you will also see the speedup knee a bit sooner.
As for HPF, there will be only one language, who's name is HPF. The next version number will be 2.0. The current level is HPF 1.1 (also known as ``full HPF'' and ``subset HPF''). The subset for 1.1 will be carried forward for Version 2.
At least, that is the current plan.
Data Parallel C extension to Standard C will likely be the closest thing to HPF in the C world. The language definition seems to be set, and there is an early product available from Pacific Sierra, called Data Parallel C. It has the flavor of *C.
I think HPF might catch on, but who knows? There is activity in the area, we have a great compiler from IBM, and experience is being accumulated.
It is time to get your feet wet, and XL HPF is on HESC!
Ironically, the demise of Thinking Machines was a boon to HPF, because CM Fortran programs had nowhere else to go.